TABLE OF CONTENTS

2.4  Continuous Growth and Decay

Goals:  

• Develop a working knowledge and understanding of the number e.

• Correctly use the compound interest formula for continuous compounding.

• Correctly use a given model for continuous decay.

Terms to know:  

·         compound interest

·         continuous compounding

·         effective annual yield

·         exponential function

·         natural exponential function

            Let’s consider another scenario  a somewhat unlikely one  but instructive none-the-less.  Suppose you have $1.00 to invest and you have a friend who will give you 100% interest.  How much money would you have after 1 year if you vary the number of compoundings?

Applying the compound interest formula and letting P = 1, and r = 1.00 and t= 1, we obtain:

Complete the following table for increasingly large values of n:

n

1

2

3

5

10

25

50

100

500

1000

Do the values of the output appear to be “leveling off?”  If so, to what number?  (You’ll have to approximate here.)

Since the set of counting numbers has infinitely many elements, we can continue the above process as long as we like.  The increase in the output changes very little, though, as n gets very large. 

We define the number e to be the number that this sequence of numbers is getting arbitrarily close to, even though we don’t know exactly what this number is.  Seem strange? 

Mathematicians use the term limit to refer to such a number and think of the number e as a limit.  In particular,  they would write:

You’ll study limits in more detail when you take calculus.  For now, what you need to know about the number e is the following:

Most historians believe that Leonhard Euler, a great 18^th century Swiss mathematician,  named this numbere.

Play around with the e button on your calculator.  What is e ²  ?  e ³ ?  What about  ?

How could you find these approximate values without using the e button ?

Example 1.   You plan to deposit money in an account giving 6% interest compounded continuously.  How much money would you have in the account after 5  years if you deposit $1000? 

For continuous compounding, use  A = Pe^rt  :                       

You would have $1349.86.

Example 2.  Which is the better deal:  An account that pays 7 % interest compounded quarterly or one that pays 6.95% compounded continuously?

SOLUTION

   For the account that pays 7 % compounded quarterly,

       use the formula  :                  A =    

      Take    to the fourth power                                

      The effective annual yield is 7.186%                                  

For the account that pays 6.95 % compounded continuously,

        Use the formula                           

        Take  e  to the 0.0695 power :                         =  P (1.07197)^t

        The effective annual yield is 7.197%.

The account paying 6.95 % interest compounded continuously is the better deal since it has a higher effective annual yield.

You can also use the table feature of your calculator to compare outputs for specific values of t .   Suppose you had $1000 to invest.  Using the variable x  instead of t , type  in

  then look at the values in the table.

Example 3.  How much money would you need to invest now in an account that gives 6% interest  compounded continuously if you want to have $1000 in this account in 4 years?

SOLUTION

Since interest is compounded continuously, we use the formula .  This time, we know the final amount, .  We also know r and t.  We plug these  numbers into the formula, like so:

The only unknown is P, so we solve the above equation for P:

So you would need to deposit $ 786.63 now into the account

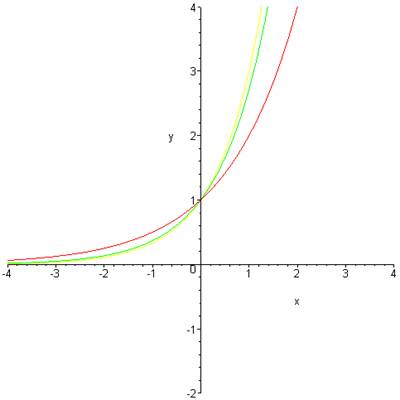
Example 4.  Using your calculator, complete the following table, then graph the exponential function .

x

e ^x

-4

-3

-2

-1

0

1

2

3

4

5

SOLUTION

As we might expect, the graph of  falls between the graphs of  and  .

The formula A= P e^rt is used whenever we wish to model ANY TYPE of continuous growth or decay.  It is often used to model population or bacteria growth, or decaying matter (as in a compost pile) and many phenomena in both the physical and business world.

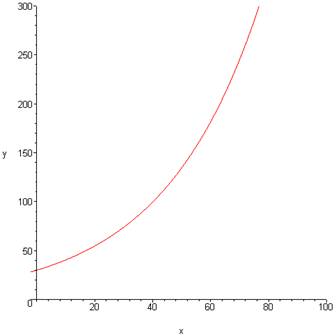
Example 5.  The approximate number of fruit flies in an experimental population after t hours is given by

a)    What is the initial number of fruit flies?

b)   How large is the population of fruit flies after 48 hours?

      c)  Sketch the graph of the function A.

SOLUTION

a)    Since the initial number occurs when , the initial number of fruit flies .

b)   After 48 hours, the number of fruit flies is   fruit flies.

c)    The independent variable is t (time) and the dependent is A, the number of fruit flies.   For this problem, it only makes sense to have positive values for t.

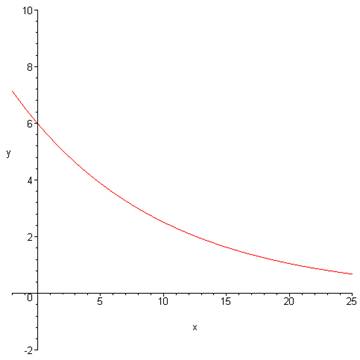
Example 6.  Medical doctors often use radioactive iodine as a tracer when diagnosing some thyroid gland disorders.  The iodine decays in such a way that after t days, the amount left is given by

where A is measured in grams. 

a)    What is the initial amount of iodine ?

b)   How much iodine remains after 15 days?

c)    Sketch a graph of the function, A.

 SOLUTION

a)    The initial amount occurs when , so the initial amount is  grams.

b)    After 15 days there is  grams.

c)    The independent variable is t (time)  and the dependent variable is A (Amount).

Checkpoint Continuous Growth and Decay

More worked examples

Homework problems

Previous Section                                                 Next Section