TABLE OF CONTENTS

3.4   Graphs and Domains of Logarithmic Functions

Goals:

·         Graph by hand a logarithmic function

·         Discuss the characteristics common to graphs of log functions with different bases

·         Write a function rule for a  give logarithmic graph

·         Find domain of given logarithmic function

Prerequisite skills and knowledge:

·         a working knowledge of logarithms to any base

Terms to know:

·         domain of a function

·         e

·         exponential function

·         logarithm

·         natural logarithm

·         sign chart

·         vertical asymptote

Concept Prep:  Graphs of log functions

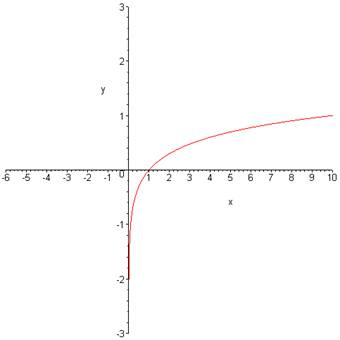
Example 1.  Make a sketch of the graph of the function given by  

First we’ll make a table of values.  Note that  is undefined, because the base, 10, is a positive number and there is no exponent that will give us :     10^??  =  -10. 

Similarly, the log of any negative number is undefined.  If we try to evaluate log(0), we have the same problem.

We say the domain of the function given by  is .

In the table below, we‘ve chosen numbers easy to work with (x = 0.01, 0.1, 1, and 10).  In the other cases, we can use our calculators to approximate the values.

Next, we plot the points and connect them.  Your graph should look something like this:

Notice that since the log of 0 is undefined, the graph hugs the vertical axis. This happens because the inputs can get really, really close to 0, but not equal 0.  We write:   

which we read “as x approaches 0 from the right.”  Notice that as these input values get very small, like , the output values get large in the negative direction.  Complete the following table to convince yourself of this fact.

We say that the vertical axis is a vertical asymptote because as   , the function values,   .

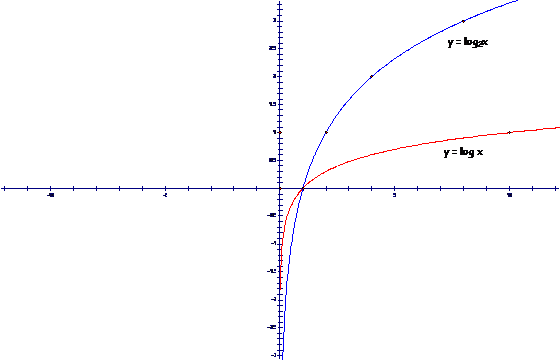
Example 2.  Make a graph of each of the functions given by  and  

Our table of values for  is the following.  Note that as with the log function base 10, only positive numbers have output values.  Note also that using powers of 2 makes calculations easy.

Note that the graph of this function is wider (farther from the x-axis) than the graph of  when the base was 10.  Discuss with your colleagues why this is so. 

Notice again that the vertical axis (y axis) is a vertical asymptote of the graph of the function  because  as   , the function values,   .

The graph of the function given by  falls in between the two graphs above:

Explain why this is so.

      Checkpoint: Graphs of Logarithmic Functions

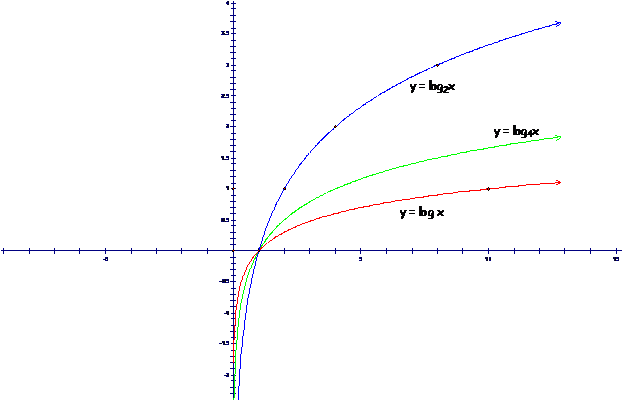
Example 3.  Note how the graph of   compares to the graph of .

Explain why this is so.

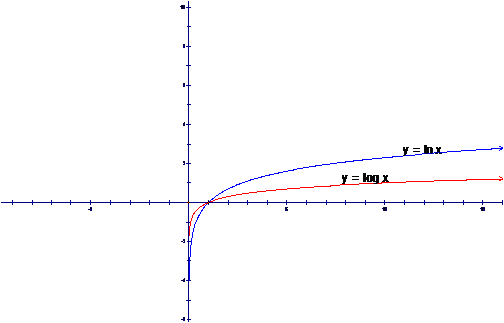
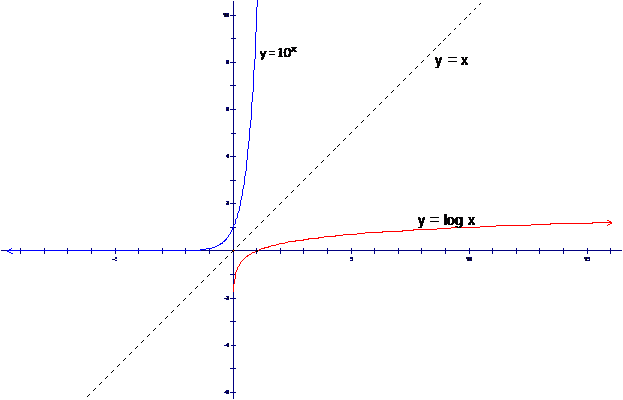
Example 4.  Compare the graphs of   and   on the same graph.  How are they related?

The graphs are mirror images of each other across the line . 

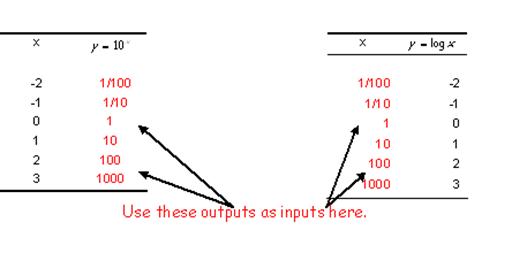
If we look at the table of values for each of the above functions,  we notice that if we use the outputs of  as inputs for , we obtain the inputs of . 

      Checkpoint: Graphs of Logarithmic Functions 2

The Domain of the Log Function

As we noticed above, the log of a negative number is undefined.  Recall that  no matter what the value of a positive base a  is,  is positive.  Convince yourself of this fact by trying to evaluate the following logarithms.

Example 5. 

a)                                                        b)      

c)                                                           d)                   

SOLUTION

a)   Using the definition of logarithm,   

     is the exponent we need to raise 10 to in order

     to obtain :                                                              

b)   Using the definition of logarithm,   

     is the exponent we need to raise 2 to in order

     to obtain  :                                                                                                      

c)  Using the definition of logarithm,   

     is the exponent we need to raise 3 to in order

     to obtain  0:                                                                                                                   

d)  Using the definition of logarithm,   

     is the exponent we need to raise e to in order

     to obtain :                                                                    

Example 6.  Find the domain of each of the following functions.

a)                                                         b)    

c)                                                d)    

e)                                       f)                                            

SOLUTION

a)     Since the log of a negative number does not exist, the domain is .

b)      

      The expression after  must be positive,

      so we set it  and solve:                                                                                                      

     The domain therefore, is         

c)                                                

       The expression after  must be positive,

        so we set it  and solve:                                          

        The domain therefore, is  

d)   

        The expression after  must be positive,

        so we set it  and solve:                                               

      The domain therefore, is . 

      Notice that some negative numbers fall in this domain.  For example,  is in the     

      domain since the expression after , which is    

      positive.

e)   

     Finding the domain for this function takes more work since the expression is non-linear.  

    You may need to refresh the use  of sign charts, which we review briefly here.  For  

    more detail, see section 2.4 of the Fundamental Mathematics V e-book.

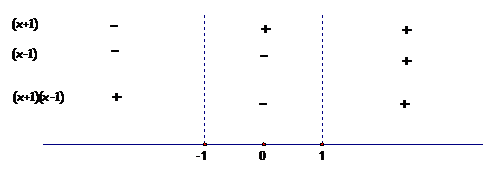
   Find the critical numbers for the function by

   setting the  expression after “log” = 0:                             

   Use these critical numbers as interval endpoints on

   a sign chart and  then use test numbers to determine the sign  

   of the factors in these intervals:

   We choose the intervals where the product  is positive.

   The domain, therefore, is  

f)    

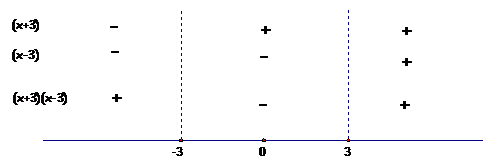
       Again we use a sign chart here:

   Find the critical numbers for the function by

   setting the  expression after “log” = 0:                             

   Use these critical numbers as interval endpoints on

   a sign chart and  then use test numbers to determine the sign  

   of the factors in these intervals:

 We choose the intervals where the product  is positive.

 The domain, therefore, is  

      Checkpoint: Domains  of Logarithmic Functions

More worked examples

Homework problems

Previous Section                                                 Next Section