TABLE OF CONTENTS

4.1        Graphs of Simple Rational Functions

Goals:  

• Understand the notion of asymptote

• Be able to accurately graph by hand the graph of the common reciprocal functions

• Graph a reflection of a reciprocal function through the x-axis

• Graph a vertical stretch or shrink of a reciprocal function

Terms to know:

·         asymptote

·         end behavior

·         decreasing function

·         increasing function

·         domain

·         range

Concept Prep:  Graphs of Simple Rational Functions  

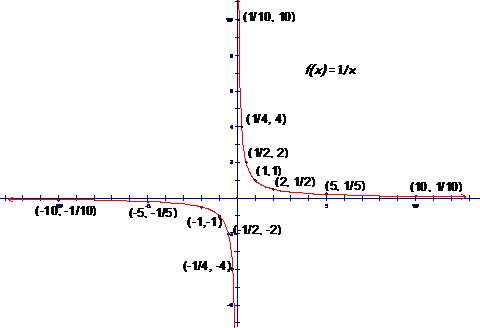
The Graph of  

In the concept prep exercise, you created various tables of values for different functions.  Here we consider the table for the function, f, given by . 

We see that as x gets very large, the outputs get close to 0, since the reciprocal of a very large number is a very small number.  (If you cut a pizza into more and more pieces, those pieces get smaller and smaller.)   In symbols, we write: as ,  and we say “as x approaches infinity,  approaches 0.” 

For positive real numbers,  

Plot these points on a set of coordinate axes.  You should notice that the points are getting very close to the x-axis  as .

Similarly, if the x values above were all negative, the output values would also be negative, but also getting close to 0. We write, as , then  and we say “as x approaches negative infinity, then  approaches 0.”

Plot these points on a set of coordinate axes.  You should notice that these points are also getting very close to the x-axis  as .

Since  as  and as , we say that the line  is the horizontal asymptote of the graph.  The end behavior (the behavior on the far left and far right side of the graph) determines this horizontal asymptote of a graph.

Horizontal Asymptote

The line  is a horizontal asymptote for a function f,  if, as the input, x,  increases or decreases without bound,  the output,  approaches 0.  Symbolically, we write:

                            or     

Symbol

Meaning

 x  decreases without bound, “x approaches negative infinity”                  

x  increases without bound ,”x  approaches infinity”

The function value tends toward h, “  approaches h”

You might notice that the same phenomenon occurs for the function g  given by  .    (as x approaches infinity  approaches 0)  and .  Thus, the line  is the horizontal asymptote of the graph.  The line  is the horizontal asymptote of the graph of a simple rational function of the form , for any n.  You might convince yourself of this fact by choosing ,  etc.

Now, we consider the output values when x gets close to zero.  Since f  is undefined at 0, we consider values of x  very close, but not equal, to 0 .  Values of x can approach 0 from either the right side (where the numbers are positive) or from the left side (where the numbers are negative).   The notation  means x is approaching 0 from the right or positive side and the notation  means x is approaching 0 from the left or negative side.  First we consider values of f(x) when .

   Note that the values f(x) are getting very large in the positive direction.  Symbolically, we write .  So, as ,  

 For positive real numbers,  

Try graphing the points in this table.  As the x-coordinates gets very close to 0, the y-coordinates increase without bound -- they get bigger and bigger.  The line  is what mathematicians call a vertical asymptote.  The word “asymptote” comes from Greek roots meaning “not falling together.”  The graph of a function and its vertical asymptote(s) do not meet. 

Similarly, if x gets closer and closer to 0 from the negative side, the output values would tend toward negative infinity. Thus in symbols we write, as .

Symbol

Meaning

 x approaches h from the  right side. 

x approaches h  from the  left side. 

Vertical Asymptote

The line  is a vertical asymptote for a function, f, if as x approaches 0, f(x) increases or decreases without bound:

as ,         or        as ,  

Note that the vertical asymptote occurs where the function is undefined.   The domain of

f, given by  , is the set of all real numbers except 0.  We write  or  to indicate this domain.

Graphing the above points on the coordinate plane and connecting them results in the following graph:

The graph of  

The range of f  is  , that is, all real numbers except 0.  The function is decreasing over its entire domain, that is, the values  are decreasing over . 

Notice that the graph has no x-intercepts or y intercepts.  Suppose we try to find these:

To find the x-intercept, set y=0:

To find the y-intercept, set :

.  Thus the graph has               

 no y-intercept.

Checkpoint 4.1 A

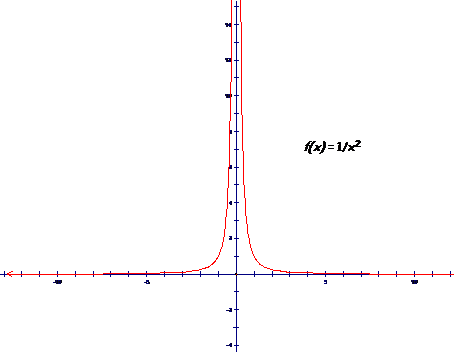
The Graph of  

Complete the following tables of values for the function g  given by .

1

-1

1

2

-2

5

-5

10

-10

50

-50

100

-100

1000

-1000

Complete the following:

a)    as  ,  

b)   as  ,   What is the horizontal asymptote?

c)    as ,  

d)      as ,    What is the vertical asymptote?

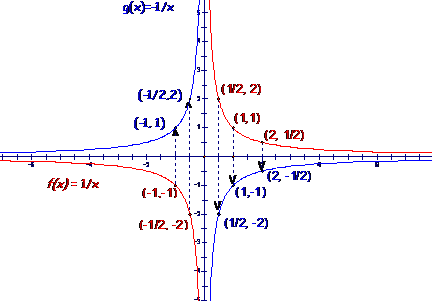
When sketching the above points and connecting them,  your graph should look something like this:

How is this graph of the function g  similar to the graph of ?   How is it different?

The domain of g is .

The range is  or .

The vertical asymptote is .

The horizontal asymptote is .

The function is increasing on  and decreasing on .

There are no x-intercepts and no y-intercepts.

Checkpoint 4.1 B

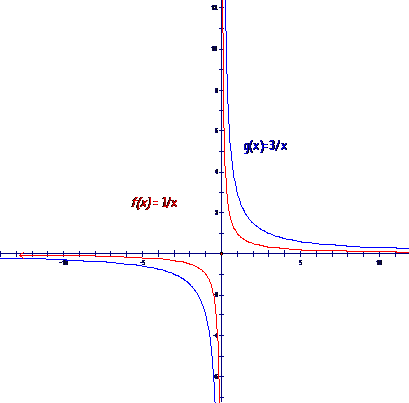
The Effect of Multiplying by a Constant, c

Recall in section 2.3 that multiplying an exponential function by a factor of c resulted in a vertical stretch of the graph.  Let’s take a look at what happens when we multiply a simple rational function by a constant, c.  We first compare tables of function values.  Let  and let .

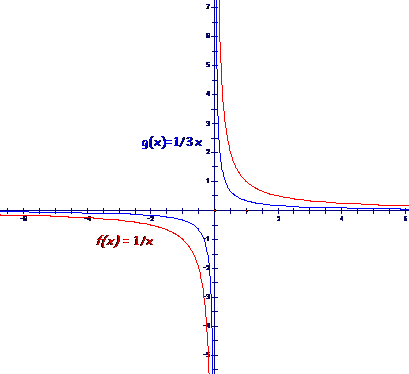
Since each output of the function g is three times the output of f, the graph of g is the graph of f stretched by a factor of 3.  Imagine holding the graph of f at the upper and lower ends and pulling it (stretching it).  The values of g decrease more slowly as  and rise faster as .  The vertical and horizontal asymptotes are the same for the graphs of both functions.   Carefully compare the plotted point for f and g so that you understand why they graphs appear as they do in the sketch below.

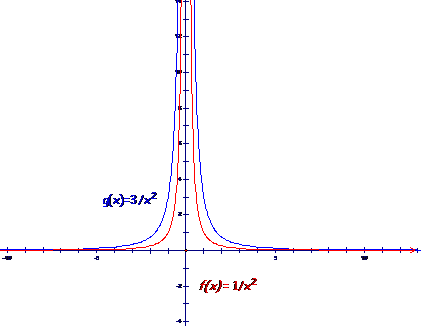
Note a similar comparison between the graphs of  and .

Using the same reasoning, let’s suppose .  Consider for example the functions f and g  given by  and . Noting that the outputs of g are one-third the outputs of f, we can compare the two graphs:

Vertical Stretch or Compression

Given a simple rational function, f,  and a new function g  such that , then:

Ø  If , then the graph of g  is a vertical stretch of the graph of f by a factor of c.

Ø  If , then the graph of g is a vertical compression of the graph of f  by a factor of c.

What if ?

How would a negative value of c  affect a graph?    Consider the function f given by  and the function g  given by .  Completing the table below clearly gives outputs for g which are opposite the outputs for f.   Before reading on, make your own sketch of the graph of .

Since each output of the function g is opposite times the     output of f, the graph of g is the graph of f reflected

   through the x-axis or “flipped upside down.”

1

1

-1

2

3

5

10

20

30

50

100

1000

Reflecting a graph

Given a function, f, and another function g  given by .  The graph of g is a reflection through the x- axis of the graph of f.

More Worked Examples

Homework problems

Previous Section                                                

Next Section