TABLE OF CONTENTS

2.3b Problem-Solving With Quadratic Functions and Equations;

       Finding Max and Min Values

Prerequisite knowledge and skills

       A working knowledge and understanding of graphs of quadratic functions

       A working knowledge and understanding of the quadratic formula

Terms to know:  

·         Discriminant

·         Leading coefficient

·         Maximum function value

·         Minimum function value

·         Parabola

·         Quadratic formula

·         Tangent

·         Vertex of a parabola

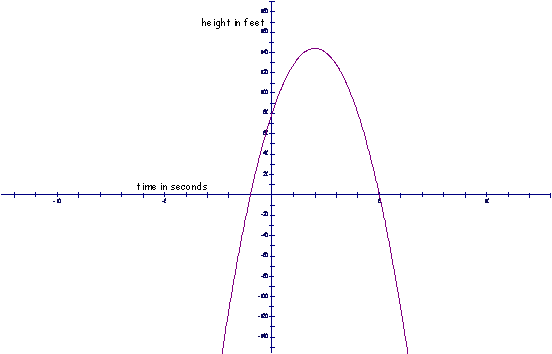
Recall the second Try It  scenario in the prep exercises for section 2.1:   The height of a fireworks display t seconds after having been launched was given by Height = .  Suppose we wanted to know the maximum height reached by the fireworks.  Where on the graph of the function would the maximum height be represented?    

This highest point on the graph of a parabola is called its vertex.

In this section we will explore the vertex of quadratic functions and develop an algebraic method for finding it.

Activity 1

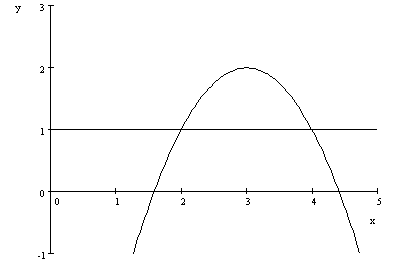
Consider the graphs of  and the horizontal line .

As the graphs intersect at two distinct points, we know that there must be two distinct values for  such that .     Use the quadratic formula to solve this equation and find these values for x.    (We know that the equation will factor, but please use the formula anyway.  You’ll see something really neat in just a bit. )

Activity 2

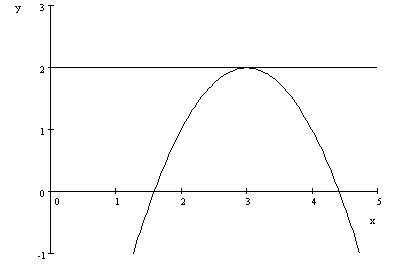
Now consider the case where . Use the quadratic formula to solve this equation, too.  

You should have found that there is only one distinct solution. This means that the graphs of  and the horizontal line  intersect at only one distinct point and that the line  is tangent to the graph of  at the point  as is shown in the following graph.

What is the maximum value for the output of this function? 

The maximum value of  is 2 and this maximum value occurs when .  Note that the term “maximum value of  ”  refers to the output  of the function.  The point  is called the vertex.

                                                                ***********

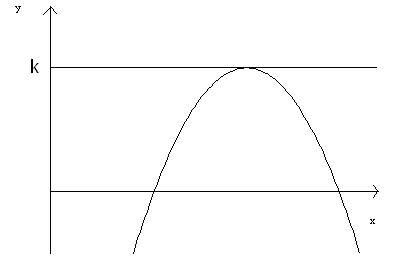
Now let us consider the general case. Let , where  and . We will assume that the graph is a parabola that “opens down”. We wish to find the maximum value of . Please note that the following will work for quadratics whose graphs are parabolas that “open up” and can be used to find minimum values.

Consider the graphs of  (again where  and  ) and the horizontal line  where . The line  is tangent to  at the vertex of the parabola. Note that there can only be one such horizontal tangent line to a parabola intersecting at exactly one point.

Now, there can only be ONE solution to the equation , as the graphs intersect at only one point. Using the quadratic formula, we have:

Note that , as  and  

Now

However, as there can only be one solution we know that

The only way this could be is if the discriminant is zero.  In other words,

Thus,  the maximum value for the output occurs if                     

This means that for any function  (  ), its maximum value (or minimum value) will occur when  and in fact, its maximum value (or minimum value) will be . Graphically this means that the coordinates of the vertex of any such quadratic function will be  

Example 1.   Determine the minimum value of  

, and  

The minimum (or maximum) value occurs when :                

Find the output, which is the minimum (or maximum) value

by substituting this value for x into the function formula:         

The vertex is therefore .

To determine whether this is a maximum or minimum value we could either graph  or choose an arbitrary value for x and compare. Let , then

We know that 16 is either a maximum or minimum value and that , so 8 must be the minimum value of the function.

You might make note of the effect of the leading coefficient  on the orientation of the graph (turned upward or turned downward).

More worked examples

Homework

Previous Section

Next Section