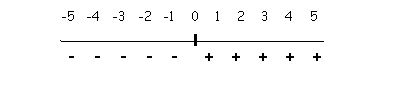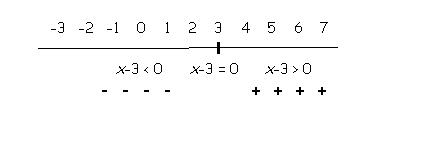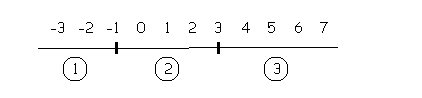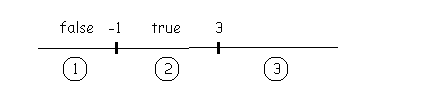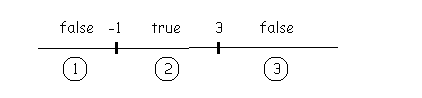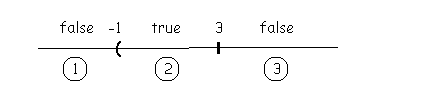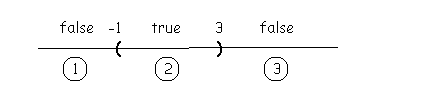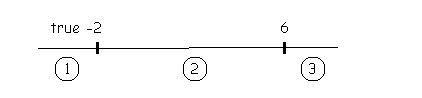BACK TO TEXT

 

2.4 Solving Quadratic Inequalities

 

There are several ways to solve quadratic inequalities. The first method examines each factor of the inequality and how various values affect them when substituted in for the variable.

 

 

METHOD 1

 

Example 1.       Solve    

 

Start by getting zero on one side of the inequality and everything else on the other side. (Why is it incorrect to say “set the inequality equal to zero”?) answer

 

The inequality is easier to solve if the quadratic term is positive.

 

                                      

 

The reason we get everything on one side of the inequality and zero on the other is because now we only have to worry about the sign of the expression on the left side. As long as  x2  2x  3  is a negative number, when a value is substituted in for x, the inequality will be true.

 

 

Notice on the number line:

 

 

Any number less than zero is a negative number and any number greater than zero is a positive number. Zero is neither positive nor negative.

 

 

Therefore, the symbolism  is referring to all negative numbers and the symbolism  is referring to all positive numbers.

 

                                                

 

Instead of just randomly filling numbers in for x  to find which values make the inequality true (which would take a lot of time), it is easier to first factor the expression  and then see how each factor is affected.

 

                         

 

                        factor

 

                         

 

There are now two quantities being multiplied together. For the inequality to be true, their product must be a negative number when values are substituted in for x.

 

                      

 

The only way the product of two numbers can be negative is if one of the factors is positive and one is negative.

 

Here are the possibilities for this problem:

 

                       

 

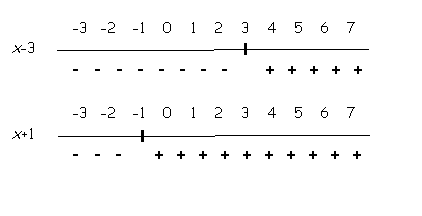
We will now look to see how every number affects each of the factors. Start by finding the numbers that when filled in for x will make each factor equal to zero.

 

                                  

 

These numbers, 3 and -1, are called “critical values”. The factors are neither positive nor negative at these numbers because they, the factors, equal zero.

 

For the factor  x-3,  at  x = 3  the factor equals zero. For any number greater than 3 that is filled in for x, the factor will end up as a positive number. For any number less than 3 that is filled in for x, the factor will end up as a negative number. Try filling in some numbers for x and seeing for yourself that this is true.

 

 

Example 2.     For ;            

   

 

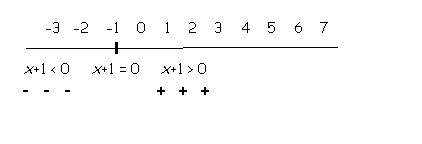
For the factor  x+1,  at  x = -1  the factor equals zero. For any number greater than -1 that is filled in for x, the factor will end up as a positive number. For any number less than -1 that is filled in for x, the factor will end up as a negative number. Try filling in some numbers for x and seeing for yourself that this is true.

 

 

Example 3.     For ;            

   

 

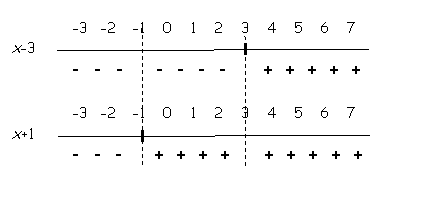
Remember, we are looking for all the numbers that will make one factor a negative number and the other factor a positive number. We will set the two number lines up one above the other and take a look:

 

 

 

 

 

 

Example 4.     

  

 

If we extend a line from each of the critical values points to the other number line, it will be easier to look at the given information:

 

 

Example 5.     

  

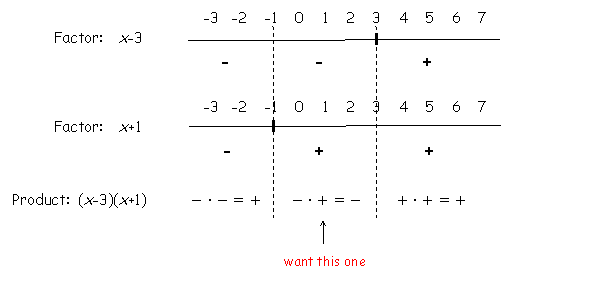
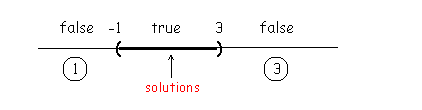
Now we can see that any number to the left of -1 will cause each of the factors to be negative, any number between -1 and 3 will cause one factor to be negative and one to be positive and any number to the right of 3 will cause each factor to be positive.

 

When two negative numbers are multiplied together, the product is positive. When two positive numbers are multiplied together, the product is positive. When a negative and a positive are multiplied together, the product is negative therefore we want the numbers between -1 and 3 so that when filled into both of the factors in the problem, the product will end up negative and less than zero.

 

 

  

 will be true when numbers between -1 and 3 are filled in for x.

 

Example 6.      Let x = 2,  which is a number between -1 and 3.

                        Then  becomes    

                                                                           which is < 0 and therefore makes the

                                                                           inequality  true.

 

Using inequality notation to write the solution:    

Using interval notation to write the solution:  (-1,3)

 

What happens if -1 or 3 is substituted in for x?  We know that each of these numbers will cause one of the factors to equal zero.  When one of the factors is zero the product will then be zero.

 

Example 7.      For    let x = 3, one of the critical numbers

 

                        The inequality then becomes   

We do not want the product to equal zero so the critical numbers are not included in the solution.

 

 

NOTE:       Critical numbers will always cause the product to equal zero when

              substituted in for the variable.

Example 8.     Solve   

                       

Get everything on one side and zero on the other (keep the x2 term positive)

 

           

 

Factor

 

         

 

This time we want the product to be positive (  ), or equal to zero.

 

Find the critical numbers (the values that make each factor equal zero)

 

         

 

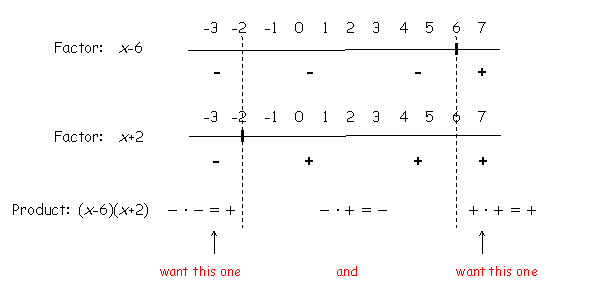
Set up the number line sign chart for each factor and the product. Look for the values that cause the product to be positive.

 

  

NOTICE:   This time there are two intervals that contain values that cause the product

                     to be positive. All the values in each of these intervals will be solutions.

 

Check the critical values to see if they will be part of the solution

For the critical value, x = 6, is  when 6 is substituted in for x ?

                                              Is  ?

                                                Is     ?

                                                Is        ?      YES!  So 6 is a solution

 

For the critical value, x = -2, is  when -2 is substituted in for x ?

                                              Is  ?

                                                Is     ?

                                                Is        ?      YES!  So -2 is a solution

 

 

Write the solution

 

Using inequality notation to write the solution:    

Using interval notation to write the solution:    

 

 

 

The second method for solving quadratic inequalities is a shortcut for the first method.

 

 

Method 2

The first three steps of this method are identical to the first three steps in Method 1

1.       Get everything on one side of the inequality sign and zero on the other. Be sure to keep the  “x2”  term positive.

2.      Factor

3.      Find the critical numbers

 

 

Example 9.    Solve    

 

Get everything on one side and zero on the other (keep the x2 term positive)

 

           

 

Factor

         

 

Find the critical values

 

         

 

Now this is where Method 2 becomes a shortcut for Method 1. Instead of setting up separate number lines for each of the factors, both critical numbers will be marked on the same number line.

           

                              

The number line has now been divided into three intervals. Look back at Example 5. Notice how after a line was extended from each of the critical values, the number line became divided into three intervals and notice that all the values in each interval affected the product in the same way  either all the values in the interval caused the product to be positive or all the values in the interval caused the product to be negative.

 

Because we know that every value in each interval affects the product in the same way, in Method 2, after marking the critical values on the number line, we will pick a test value from each interval to represent that particular interval and see how the product is affected. Let’s label the intervals 1, 2 and 3 to make them easier to refer to.

           

                              

 

From Interval 1, let x be the test value -2. Remember, it doesn’t matter which value is picked as the test value because all the values in this interval will affect the product in

the same way, from Interval 2, let x be the test value 0 (my favorite test value) and from Interval 3, let x = 4. Now fill each one of these test values into the original inequality - not the factored inequality - the original inequality, and see whether the inequality is then true or not.

 

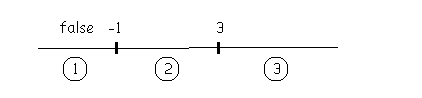
For Interval 1, if x = -2 then    becomes

                  

 

Write the word “false” above Interval 1.

 

                              

 

 

For Interval 2, if x = 0 then    becomes                                           

                                                               

                                                                                   

                                                                      This inequality IS true therefore, all

                                                                      the values in Interval 2 will be solutions

                                                                      for the inequality.

                                                                      

 

Write the word “true” above Interval 2.

 

                              

 

         

For Interval 3, if x = 4 then    becomes   

                  

 

Write the word “false” above Interval 3.

 

                              

 

If you want, you can now test the critical numbers by substituting them in for the variable one at a time to see how they affect the inequality. They will, however, always make one side of the inequality equal to the other side.

 

For the critical number -1,  if  x = -1  then    becomes    

                                                                                          

                                                      This inequality is NOT

                                                                                       true therefore, 1 is not

                                                                                       one of the solutions

                                                                                       for the inequality.

 

Put a parenthesis (which means “not included”) on this number on the number line.

 

 

                              

 

 

 

For the critical number 3,  if  x = 3  then    becomes    

 

                                                                                     

                                                        This inequality is NOT

                                                                                         true therefore, 3 is not

                                                                                         one of the solutions either.

                                                                                         

Put a parenthesis also on this number on the number line.

 

                              

 

The correct solution for this inequality is all the numbers in Interval 2, the interval

where the word “true” is written. Remember, however, that the critical numbers are not part of the solution.

 

                              

 

In inequality notation, the solution is  -1 < x < 3. In interval notation, the solution is (-1,3).

 

 

Example 10.     Solve   

 

Get everything on one side and zero on the other (keep the x2 term positive)

 

         

 

 

 

Factor

                         

 

 

Find the critical numbers for each factor

 

                        For x-6,  x = 6;   for x+2,  x = -2

 

 

Mark the critical numbers on the number line to create intervals

 

                             

 

Pick a test value from each interval to represent that interval. Fill it into the original inequality for the variable and see if it is a solution or not.

 

For Interval 1, let x = -3 then    becomes                                           

                                                               

                                                                                   

                                                                      This inequality IS true therefore, all

                                                                      the values in Interval 1 will be solutions

                                                                      for the inequality.

                                                                      

 

Write the word “true” above Interval 1.

 

                               

 

 

 

 

 

For Interval 2, let x = 0  then    becomes                                           

                                                               

                                                                                   

                                                                      This inequality is NOT true therefore,

                                                                      all the values in Interval 2 will not be

                                                                      solutions for the inequality.                                      

 

Write the word “false” above Interval 2.

 

                               

 

 

For Interval 3, let x = 7  then    becomes                                           

                                                               

                                                                                   

                                                                      This inequality IS true therefore, all

                                                                      the values in Interval 1 will be solutions

                                                                      for the inequality.

                                                                      

 

Write the word “true” above Interval 3.

 

                               

 

 

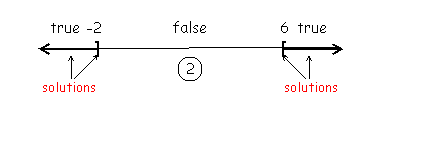
Check the critical numbers to see if they are solutions also by filling them into the original inequality for the variable.

 

 

For the critical number -2,  if  x = -2  then    becomes    

 

                                                                                     

                                                        This inequality IS true

                                                                                         therefore, -2 is one of

                                                                                         the solutions.

 

                                                                                         

Put a bracket (which means “included”) on this number on the number line.

 

                               

 

 

For the critical number 6,  if  x = 6   then    becomes    

 

                                                                                     

                                                        This inequality IS true

                                                                                         therefore, 6 is also one

                                                                                         of the solutions.

 

                                                                                         

Put a bracket (which means “included”) on this number on the number line.

 

                               

 

The correct solution for this inequality is all the numbers in Interval 1 and Interval 3, the intervals where the word “true” is written. In this example, the critical numbers are also part of the solution.

 

 

                               

In inequality notation, the solution is  .  In interval notation, the solution is

.

 

 

 

Method 3 is a graphical approach to solving the quadratic inequality

 

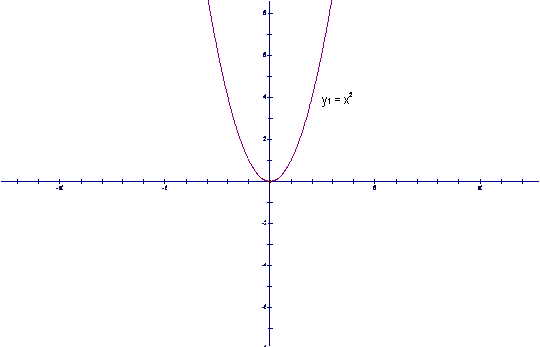
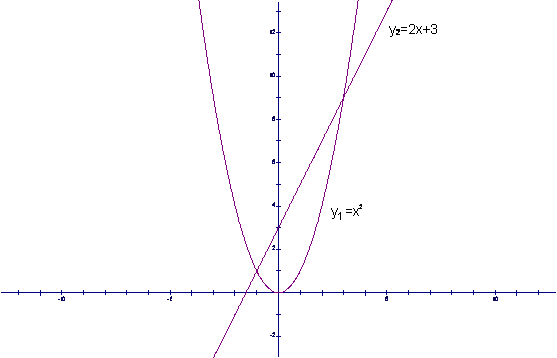
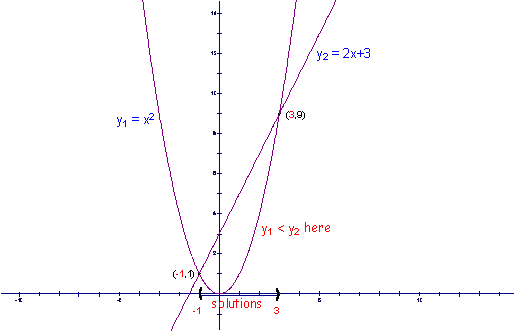
Let  y1 = x2   and   y2 = 2x + 3

 

The graph of y1 = x2   is a parabola because it is a quadratic equation.

 

              

        

 

 

Y2 = 2x + 3  is a linear equation and so its graph is a straight line with a slope of 2 and a

y-intercept at (0,3).

        

 

 

 

Now plot these two graphs on the same set of axes.

 

 

       

 

When solving the inequality , you are actually solving the inequality  where  stands for the  values (or outputs) of the equation   after various values are filled in for x (or the input) and  stands for the  values (or outputs) of the equation   after various values are filled in for x (or the input).

 

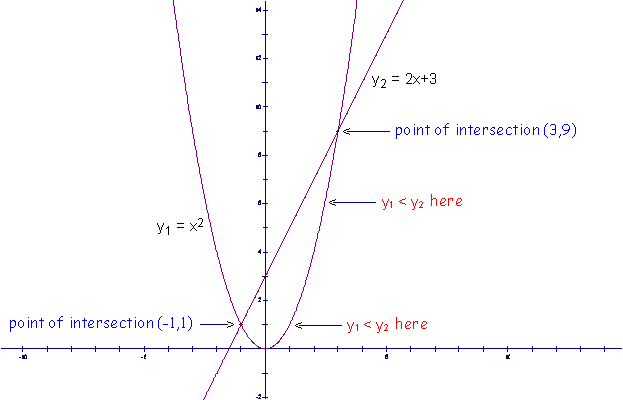
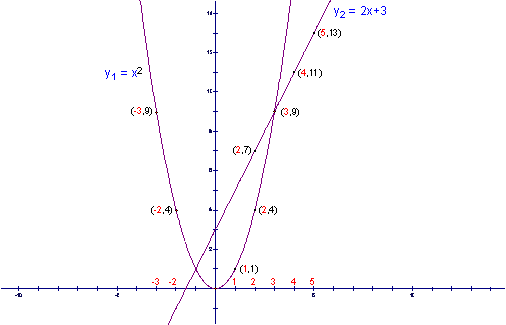
When solving the inequality , all you need to do is look at the graphs of the two equations and find where the  values are less than (or below) the  values.

 

 

 

 

With the above two graphs, it is rather easy to see that the graphs intersect at the points (-1,1) and (3,9).  At these points,  actually equals . Between the points (-1,1) and (3,9), the graph of  is below the graph of  and so between the points (-1,1) and (3,9), all the  values are less than the  values.

 

The only thing left to do now to solve the inequality  is to determine which x’s  were used to draw this part of the graph.  Look at the points listed on the following graphs.  Notice that for each point, the x of the point that was used to get the y is the x on the x-axis that lies directly below the point.

                 

 

 

Can you see on the graphs below, then, that the x’s that cause the graph of  to be less than (or below) the graph of  are the x’s in between  x = -1 and  x = 3.  These are the x’s that are the solutions to the inequality .

                         

               

 

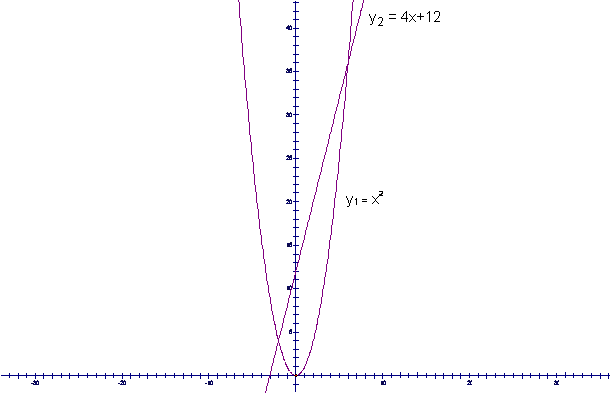
In inequality notation, the solution is .  In interval notation, the solution is (-1,3).

Example 11.     Solve   using Method 3

 

Let y1 = x2   and   y2 = 4x+12

 

Graph these two equations on the same set of axes

 

 

 

 

You must now find where the two graphs intersect

 

When the graphs intersect each other, the y  values of the graphs are identical at these points:  y1 = y2 .  So set the equations equal to each other and solve for x.

 

                         

                               

 

To find the y  values that correspond to these x’s just plug the x’s into either equation.  It doesn’t matter which equation because they will both end up equaling the same number. Test it for yourself.

 

At  x = 6,     y1 = x2  becomes  y1 = (6)2                    y2 = 4x+12  becomes  y2 = 4(6)+12

                                                       = 36                                                              = 24+12

                                                                                                                             = 36

 

                                                       See, identical answers.

 

At  x = -2    y1 = (-2)2 = 4

 

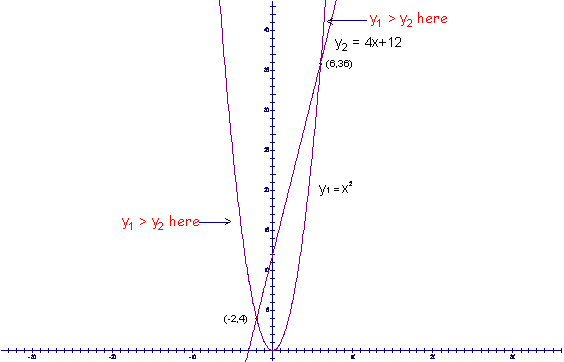
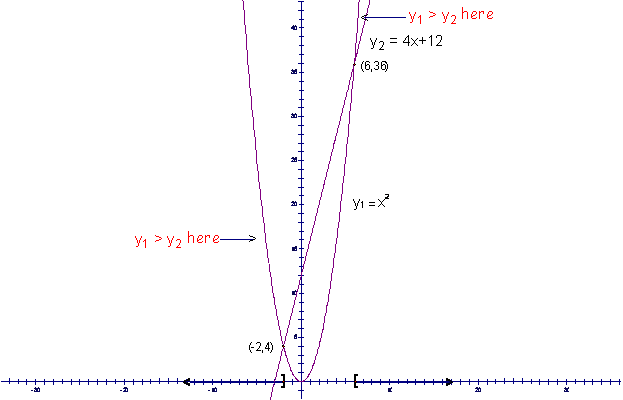
The points of intersection for the graphs are at (-2,4) and (6,36).

 

Now determine where  or  y1 = x2 is above y2 = 4x+12.

 

      

    

Looking at the above graphs, it can be seen that y1 is above y2 to the left of the point (-2,4)

and to the right of the point (6,36).  Since in the original problem, you are trying to find the x’s that cause x2 to be greater than or equal to 4x+12, or the x’s used to construct the graphs that cause y1 to be greater than or equal to y2, the solution to the problem in inequality notation is  .  In interval notation, the solution is  .

 

 

 

 

                                                       solutions                   solutions

 

 

BACK TO TEXT